A Função do Segundo Grau: Uma Abordagem Prática: Aplicação Da Função Do Segundo Grau Na Vida Real Exemplos
Aplicação Da Função Do Segundo Grau Na Vida Real Exemplos – A função do segundo grau, também conhecida como função quadrática, é uma ferramenta matemática poderosa com aplicações vastas em diversas áreas do conhecimento. Sua forma geral, f(x) = ax² + bx + c, onde a, b, e c são constantes reais e a ≠ 0, define uma parábola no plano cartesiano. O coeficiente a determina a concavidade da parábola (para cima se a > 0, para baixo se a < 0), enquanto o vértice representa o ponto de máximo ou mínimo da função, dependendo da concavidade.
A compreensão desses elementos é fundamental para a aplicação eficaz da função em situações reais.
A Forma Geral e Elementos da Função do Segundo Grau
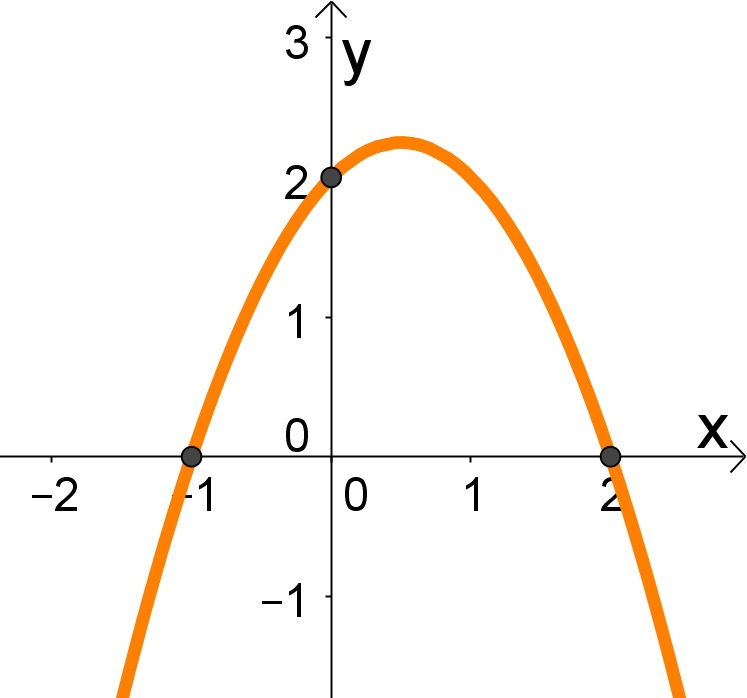
A equação f(x) = ax² + bx + c descreve completamente a função do segundo grau. O coeficiente ‘a’ define a abertura e a concavidade da parábola. Um valor positivo de ‘a’ indica uma parábola que se abre para cima, enquanto um valor negativo indica uma parábola que se abre para baixo. O coeficiente ‘b’ influencia a posição horizontal do vértice da parábola, e o coeficiente ‘c’ representa o ponto de intersecção da parábola com o eixo y.
O vértice, ponto de máximo ou mínimo da função, possui coordenadas que podem ser calculadas através das fórmulas xv = -b/2a e yv = f(x v) . Geometricamente, o vértice representa o ponto de maior ou menor valor da função, sendo crucial para a análise de problemas de otimização.
Aplicações em Engenharia e Arquitetura
A função do segundo grau é fundamental em projetos de engenharia e arquitetura, principalmente no cálculo de trajetórias e no desenho de estruturas curvas.
| Tipo de Projétil | Equação da Trajetória (aproximada) | Alcance Máximo (aproximado) | Altura Máxima (aproximada) |
|---|---|---|---|
| Bola de futebol | y = -0.01x² + x | 100m | 25m |
| Bala de canhão | y = -0.005x² + 2x | 400m | 200m |
| Foguete | y = -0.001x² + 5x | 5000m | 1250m |
| Pedra lançada | y = -0.02x² + 0.5x | 12.5m | 3.125m |
Note que as equações e valores apresentados na tabela são aproximações para fins ilustrativos. Valores reais dependerão de diversos fatores, como velocidade inicial, ângulo de lançamento, e resistência do ar.
Desenho de Pontes e Arcos Parabólicos
Pontes e arcos parabólicos são exemplos clássicos de aplicação da função do segundo grau na arquitetura. A forma parabólica proporciona uma distribuição eficiente de peso e tensões, resultando em estruturas robustas e estáveis. Por exemplo, uma ponte com um arco parabólico de 100 metros de vão e 20 metros de altura pode ser modelada por uma função do segundo grau, onde o vértice se encontra no ponto mais alto do arco.
A equação exata dependeria das especificações do projeto, mas o conceito fundamental reside na modelagem da curva do arco através de uma parábola. Comparativamente, outras funções, como funções exponenciais ou trigonométricas, poderiam ser utilizadas em certos casos, mas a parábola muitas vezes oferece uma solução mais simples e eficiente para este tipo de estrutura.
Aplicações em Economia e Finanças, Aplicação Da Função Do Segundo Grau Na Vida Real Exemplos
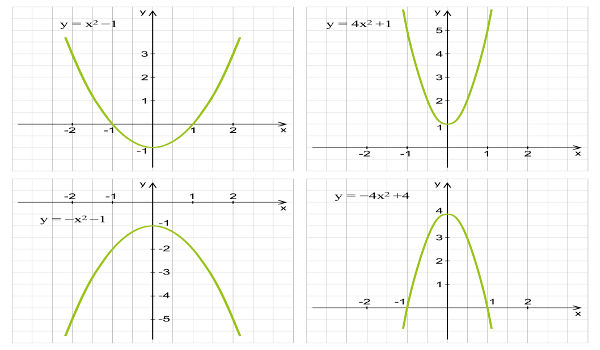
A função do segundo grau encontra aplicações importantes na modelagem de fenômenos econômicos, permitindo a análise de cenários e a tomada de decisões mais informadas.
- Modelagem do lucro de uma empresa: O lucro (L) pode ser expresso em função da quantidade produzida (x) através de uma equação do segundo grau, considerando custos fixos, custos variáveis e preço de venda. Um exemplo seria: L(x) = -0.1x² + 10x – 50. O ponto máximo desta parábola representa o nível de produção que maximiza o lucro.
- Determinação do ponto de equilíbrio: O ponto de equilíbrio em um mercado, onde a receita iguala o custo, pode ser determinado resolvendo a equação do segundo grau que representa a receita e o custo. Variáveis como preço de venda, custo fixo e custo variável são cruciais nesse cálculo.
- Simplificações e Adaptações: Em cenários econômicos complexos, o modelo de função do segundo grau pode ser simplificado ou adaptado, por exemplo, através de aproximações lineares em regiões específicas da curva, para melhor representar a realidade.
Aplicações em Física e outras Ciências
Em física, a função do segundo grau descreve o movimento uniformemente variado, onde a aceleração é constante. A posição (s) de um objeto em função do tempo (t) é dada por s(t) = s0 + v 0t + (1/2)at² , onde s0 é a posição inicial, v0 é a velocidade inicial, e a é a aceleração. O gráfico dessa função é uma parábola, cuja concavidade depende do sinal da aceleração.
A velocidade é a derivada da posição em relação ao tempo, e a aceleração é a derivada da velocidade em relação ao tempo.
Em contraste com modelos lineares, a função quadrática permite modelar situações onde a taxa de variação não é constante, como no caso da queda livre de um corpo sob a ação da gravidade. Outros modelos, como os exponenciais, são adequados para descrever fenômenos com crescimento ou decaimento exponencial, enquanto os modelos oscilatórios (trigonométricos) descrevem movimentos periódicos.
Um exemplo de aplicação envolvendo energia potencial gravitacional seria calcular a energia potencial de um objeto de massa ‘m’ a uma altura ‘h’ acima do solo, dada pela equação Ep = mgh , onde ‘g’ é a aceleração da gravidade. Embora essa equação seja linear em relação à altura, a trajetória do objeto em queda livre é descrita por uma função quadrática, conectando diretamente a energia potencial à posição do objeto durante sua queda.
Construindo Modelos com a Função do Segundo Grau
A construção de modelos matemáticos utilizando a função do segundo grau requer a identificação cuidadosa das variáveis e a formulação de uma equação que represente o fenômeno em questão.
- Área de um terreno retangular: Se a soma dos lados de um terreno retangular é constante (2p), a área (A) pode ser representada por A(x) = x(p-x) = -x² + px, onde x é um dos lados do retângulo. Esta é uma função do segundo grau, cujo ponto máximo representa as dimensões que maximizam a área do terreno.
- Altura máxima de um objeto lançado: A altura (h) atingida por um objeto lançado verticalmente para cima, considerando a gravidade (g), é dada por h(t) = v0t – (1/2)gt² , onde v0 é a velocidade inicial e t é o tempo. O vértice desta parábola representa a altura máxima atingida pelo objeto.
- Guia passo-a-passo: A construção de modelos com a função do segundo grau envolve: (1) Identificação das variáveis e relações entre elas; (2) Formulação de uma equação do segundo grau que represente o problema; (3) Resolução da equação para encontrar os valores desejados; (4) Interpretação dos resultados no contexto do problema original.
Em resumo, a função do segundo grau transcende os limites da sala de aula, revelando-se uma ferramenta essencial para modelar e compreender uma ampla gama de fenômenos reais. De estruturas arquitetônicas a previsões econômicas, sua aplicação prática demonstra sua versatilidade e importância em diferentes campos científicos e tecnológicos. Dominar seus conceitos e aplicações abre um leque de possibilidades, permitindo a resolução de problemas complexos e o desenvolvimento de soluções inovadoras em diversas áreas.
A próxima vez que você observar uma ponte arqueada ou analisar um gráfico de lucros, lembre-se do poder discreto, porém fundamental, da função do segundo grau.

