Relações Métricas No Triângulo Retângulo Exemplos mergulha no estudo das relações matemáticas que governam os lados e ângulos de um triângulo retângulo, explorando conceitos fundamentais como o Teorema de Pitágoras, relações trigonométricas e a aplicação prática desses princípios.
Esta investigação aprofunda o entendimento das relações métricas no triângulo retângulo, desvendando como o Teorema de Pitágoras permite calcular a hipotenusa ou um cateto, e como as relações trigonométricas (seno, cosseno, tangente) são usadas para determinar os ângulos e lados.
Através de exemplos práticos e tabelas elucidativas, o estudo demonstra a aplicabilidade dessas relações em diversos cenários, desde a resolução de problemas geométricos até a aplicação em áreas como engenharia e arquitetura.
Relações Métricas no Triângulo Retângulo
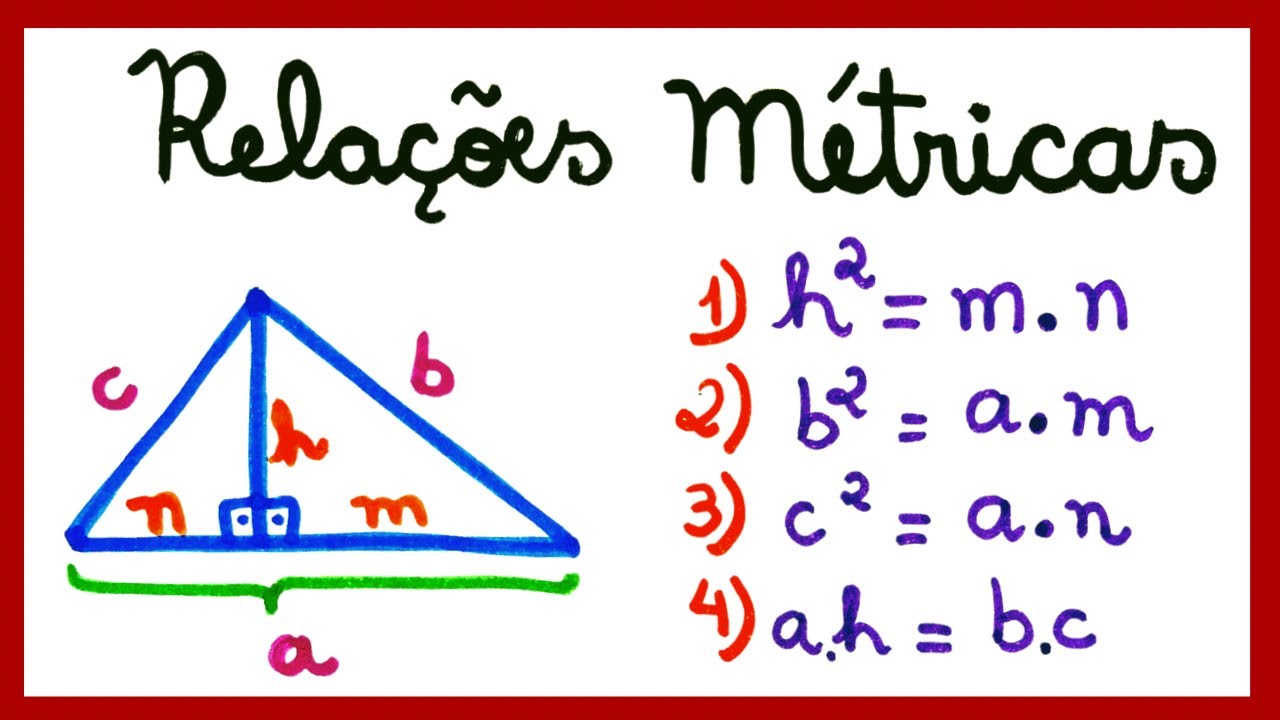
O estudo das relações métricas no triângulo retângulo é fundamental na geometria, pois permite estabelecer relações entre os lados e os ângulos desse tipo de triângulo. Essas relações são amplamente utilizadas em diversas áreas, como engenharia, arquitetura, física e matemática.
Teorema de Pitágoras
O Teorema de Pitágoras é uma das relações métricas mais importantes no triângulo retângulo. Ele estabelece que a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
Em um triângulo retângulo, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
- Catetos:Os lados que formam o ângulo reto do triângulo retângulo.
- Hipotenusa:O lado oposto ao ângulo reto, sendo o maior lado do triângulo.
O Teorema de Pitágoras pode ser expresso matematicamente pela seguinte fórmula:
a² + b² = c²
onde:
- a e b são os comprimentos dos catetos
- c é o comprimento da hipotenusa
Relações Trigonométricas
As relações trigonométricas seno, cosseno e tangente são utilizadas para determinar as relações entre os ângulos e os lados de um triângulo retângulo.
- Seno (sen):A razão entre o cateto oposto ao ângulo e a hipotenusa.
- Cosseno (cos):A razão entre o cateto adjacente ao ângulo e a hipotenusa.
- Tangente (tg):A razão entre o cateto oposto ao ângulo e o cateto adjacente ao ângulo.
Essas relações podem ser expressas pelas seguintes fórmulas:
sen α = a/c
cos α = b/c
tg α = a/b
onde:
- α é o ângulo considerado
- a é o cateto oposto ao ângulo α
- b é o cateto adjacente ao ângulo α
- c é a hipotenusa
Relações entre as Projeções dos Catetos
As projeções dos catetos são os segmentos que os catetos formam sobre a hipotenusa.
- Projeção do cateto a sobre a hipotenusa:m
- Projeção do cateto b sobre a hipotenusa:n
As relações entre as projeções dos catetos e os lados do triângulo retângulo são:
a² = cm
b² = cn
ab = mn
onde:
- a e b são os comprimentos dos catetos
- c é o comprimento da hipotenusa
- m e n são as projeções dos catetos sobre a hipotenusa
Aplicações Práticas
As relações métricas no triângulo retângulo são amplamente utilizadas em diversas áreas, como:
- Engenharia:Cálculo de estruturas, pontes, edifícios e outras construções.
- Arquitetura:Projetos de casas, edifícios, pontes e outras construções.
- Física:Cálculo de vetores, forças, movimentos e outros conceitos físicos.
- Navegação:Determinação de distâncias, direções e posições.
- Astronomia:Cálculo de distâncias e posições de estrelas e planetas.
Aplicações das Relações Métricas em Triângulos Retângulos
As relações métricas em triângulos retângulos, como o Teorema de Pitágoras e as relações trigonométricas, são ferramentas poderosas para resolver problemas que envolvem triângulos retângulos. Essas relações permitem calcular lados, ângulos e outras medidas importantes em situações práticas.
Aplicações do Teorema de Pitágoras
O Teorema de Pitágoras estabelece que em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. Essa relação é fundamental para determinar a medida da hipotenusa ou de um cateto, conhecendo as medidas dos outros lados.
Em um triângulo retângulo ABC, com ângulo reto em C, a hipotenusa é a, e os catetos são b e c: a² = b² + c².
Exemplo:Um triângulo retângulo possui catetos com medidas de 3 cm e 4 cm. Para calcular a medida da hipotenusa, podemos utilizar o Teorema de Pitágoras:a² = b² + c²a² = 3² + 4²a² = 9 + 16a² = 25a = √25a = 5 cmPortanto, a hipotenusa do triângulo retângulo mede 5 cm.
Aplicações das Relações Trigonométricas
As relações trigonométricas, seno (sen), cosseno (cos) e tangente (tan), são definidas como razões entre os lados de um triângulo retângulo e seus ângulos. Essas relações são usadas para determinar os ângulos e os lados de um triângulo retângulo, conhecendo alguns valores.
Em um triângulo retângulo ABC, com ângulo reto em C, o ângulo agudo A é considerado:sen A = cateto oposto / hipotenusacos A = cateto adjacente / hipotenusatan A = cateto oposto / cateto adjacente
Exemplo:Um triângulo retângulo possui um ângulo de 30° e um cateto oposto a esse ângulo com medida de 5 cm. Para determinar a medida da hipotenusa, podemos usar a relação trigonométrica seno:sen 30° = cateto oposto / hipotenusa
/2 = 5 cm / hipotenusa
hipotenusa = 5 cm / (1/2)hipotenusa = 10 cmPortanto, a hipotenusa do triângulo retângulo mede 10 cm.
Resolução de Problemas com Relações Métricas
As relações métricas em triângulos retângulos podem ser usadas para resolver uma variedade de problemas práticos. A tabela a seguir apresenta alguns exemplos:
| Problema | Relações Métricas Utilizadas | Passos para a Resolução |
|---|---|---|
| Determinar a altura de um edifício, conhecendo a distância do observador até o edifício e o ângulo de elevação. | Tangente | 1. Identificar o triângulo retângulo formado pela altura do edifício, a distância do observador e a linha de visão.
|
| Calcular a distância entre dois pontos, conhecendo a distância de cada ponto a um ponto de referência comum e o ângulo formado entre as duas linhas de distância. | Lei dos Cossenos | 1. Identificar o triângulo formado pelos dois pontos e o ponto de referência comum.
|
| Determinar a área de um terreno triangular, conhecendo a base e a altura do triângulo. | Área do Triângulo | 1. Identificar o triângulo retângulo formado pela base, a altura e o lado do triângulo.
|
Relações Métricas e Semelhança de Triângulos: Relações Métricas No Triângulo Retângulo Exemplos
A relação entre as relações métricas e a semelhança de triângulos é fundamental para a resolução de problemas envolvendo triângulos retângulos. As relações métricas, como o Teorema de Pitágoras e as relações entre os lados e as alturas de um triângulo retângulo, são diretamente derivadas da semelhança de triângulos.
Comparação das Relações Métricas em Triângulos Semelhantes
A semelhança de triângulos implica que os ângulos correspondentes são iguais e os lados correspondentes são proporcionais. Essa proporcionalidade entre os lados de triângulos semelhantes é a base para as relações métricas.
- Teorema de Pitágoras:Em triângulos retângulos semelhantes, a razão entre os quadrados dos lados correspondentes é constante. Seja a, b e c os lados de um triângulo retângulo e a’, b’ e c’ os lados de um triângulo retângulo semelhante, então:
a²/a’² = b²/b’² = c²/c’²
- Relações entre os lados e as alturas:As relações entre os lados e as alturas de um triângulo retângulo também são mantidas em triângulos semelhantes. Por exemplo, a razão entre a altura relativa à hipotenusa e a hipotenusa é constante em triângulos semelhantes. Seja h a altura relativa à hipotenusa em um triângulo retângulo e h’ a altura relativa à hipotenusa em um triângulo retângulo semelhante, então:
h/h’ = c/c’
Ilustração da Relação entre as Relações Métricas e a Semelhança de Triângulos
Considere dois triângulos retângulos semelhantes, ABC e A’B’C’, onde C e C’ são os ângulos retos. Seja h a altura relativa à hipotenusa em ABC e h’ a altura relativa à hipotenusa em A’B’C’.
Devido à semelhança, os triângulos ABC e A’B’C’ possuem ângulos correspondentes iguais. Portanto, os ângulos A e A’, B e B’ são iguais. Além disso, os lados correspondentes são proporcionais:
AB/A’B’ = BC/B’C’ = AC/A’C’
Observando os triângulos retângulos menores formados pela altura h em ABC e h’ em A’B’C’, podemos notar que eles também são semelhantes. Isso ocorre porque os ângulos correspondentes são iguais (ângulo reto, ângulo A e ângulo B). Portanto, os lados correspondentes desses triângulos menores também são proporcionais:
AC/A’C’ = h/h’
Combinando as proporções acima, obtemos:
h/h’ = c/c’
Essa relação demonstra que a razão entre a altura relativa à hipotenusa e a hipotenusa é constante em triângulos semelhantes. Isso é apenas um exemplo de como as relações métricas são derivadas da semelhança de triângulos.
A compreensão das relações métricas no triângulo retângulo abre portas para uma vasta gama de aplicações práticas. O estudo aprofunda o conhecimento sobre a geometria, fornecendo ferramentas essenciais para a resolução de problemas em áreas como engenharia, arquitetura, física e matemática.
As relações métricas no triângulo retângulo representam um pilar fundamental da geometria, oferecendo um sistema estruturado para a análise e resolução de problemas que envolvem figuras geométricas.

