Sistemas Lineares | Lista De Exercícios Resolvidos: Este material aborda a resolução de sistemas lineares, explorando métodos como Gauss, Gauss-Jordan e Cramer. A análise inclui a comparação da eficiência computacional desses métodos e a interpretação geométrica das soluções, demonstrando a versatilidade da álgebra linear na modelagem de problemas diversos, desde aplicações em engenharia até a formulação de modelos econômicos.
A lista de exercícios resolvidos fornece exemplos práticos e detalhados, facilitando a compreensão dos conceitos e a aplicação das técnicas aprendidas.
A compreensão de sistemas lineares é fundamental em diversas áreas da ciência e da engenharia. Esta lista de exercícios visa consolidar o conhecimento teórico através da prática, abordando diferentes tipos de sistemas e suas respectivas soluções, incluindo casos com solução única, infinitas soluções e sem solução. A apresentação de exemplos práticos em contextos reais reforça a aplicabilidade e a importância do domínio desta ferramenta matemática.
Métodos de Resolução de Sistemas Lineares
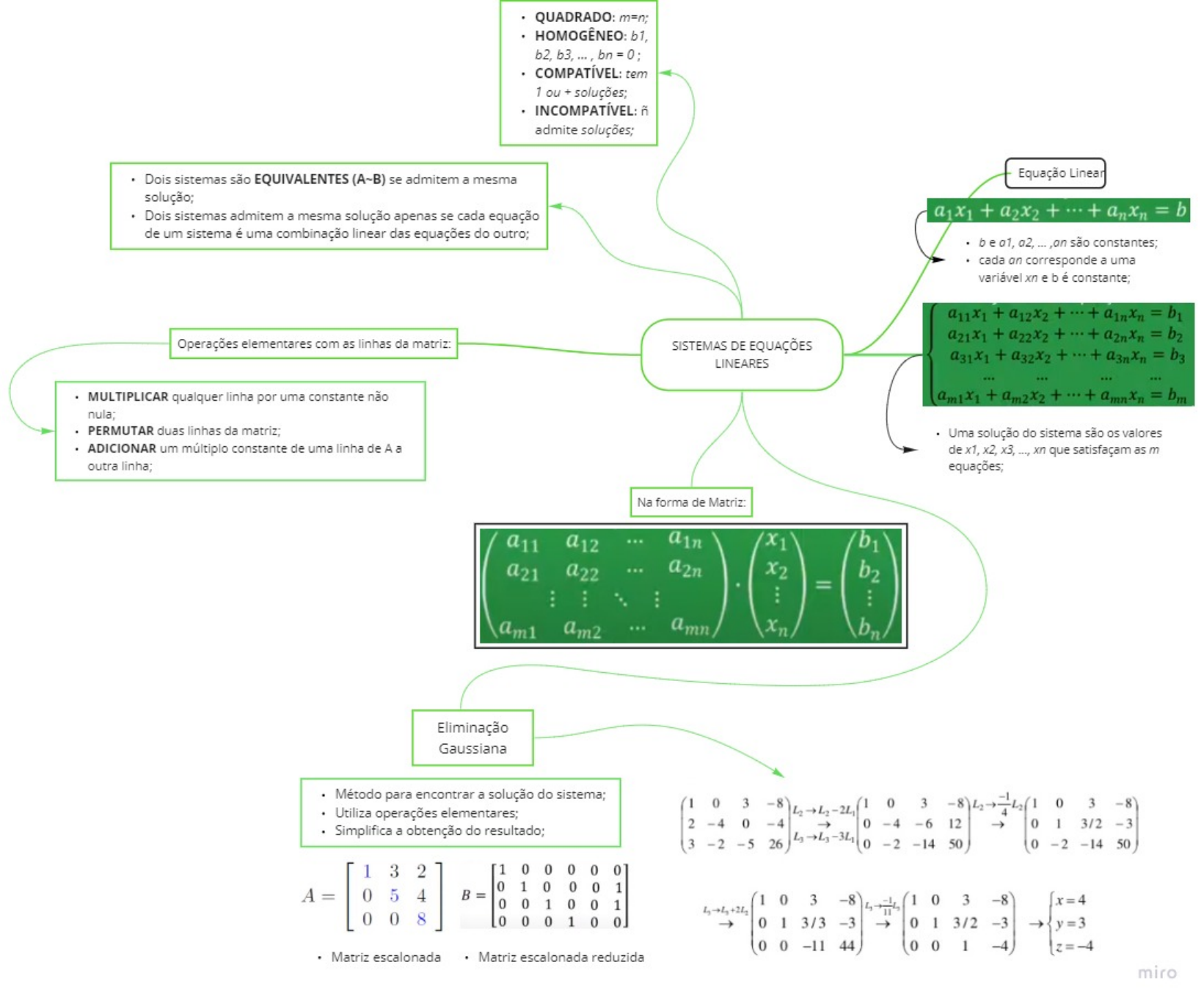
A resolução de sistemas lineares é uma tarefa fundamental em diversas áreas da ciência e engenharia. Existem diversos métodos para encontrar a solução, cada um com suas vantagens e desvantagens em termos de eficiência computacional e facilidade de implementação. Esta seção detalha alguns dos métodos mais comuns, incluindo a eliminação de Gauss, Gauss-Jordan e a regra de Cramer.
Eliminação de Gauss e Gauss-Jordan
A eliminação de Gauss e o método de Gauss-Jordan são algoritmos para resolver sistemas lineares através da manipulação de matrizes. Ambos os métodos se baseiam na transformação da matriz aumentada do sistema em uma forma triangular superior (Gauss) ou em uma forma escalonada reduzida (Gauss-Jordan).
A eliminação de Gauss consiste em transformar o sistema linear em um sistema equivalente com uma matriz triangular superior, utilizando operações elementares sobre as linhas da matriz aumentada. Após obter a forma triangular, a solução é encontrada através da substituição regressiva.
O método de Gauss-Jordan, por sua vez, continua o processo de eliminação até obter a forma escalonada reduzida, onde a matriz dos coeficientes se torna a matriz identidade. Neste caso, a solução é obtida diretamente da matriz aumentada.
A seguir, são apresentados os passos de cada método, ilustrados com exemplos:
| Passo | Eliminação de Gauss | Gauss-Jordan | Exemplo (Matriz Aumentada: [2 1 | 8; 1 3 | 11]) |
|---|---|---|---|
| 1 | Escolha um pivô (elemento não nulo). | Escolha um pivô (elemento não nulo). | Pivô: 2 |
| 2 | Utilize operações elementares para zerar os elementos abaixo do pivô. | Utilize operações elementares para zerar os elementos abaixo e acima do pivô, normalizando o pivô para 1. | L2 ← L2 – (1/2)L1 (resultando em [2 1 | 8; 0 5/2 | 7]) |
| 3 | Repita o processo para os pivôs subsequentes. | Repita o processo para todos os pivôs. | Substituição regressiva (Gauss): y = 14/5, x = 18/5; Gauss-Jordan: [1 0 | 3; 0 1 | 14/5] |
| 4 | Resolva o sistema triangular superior por substituição regressiva. | A solução é lida diretamente da matriz aumentada. | x = 3, y = 14/5 |
Comparação da Eficiência de Gauss e Gauss-Jordan, Sistemas Lineares | Lista De Exercícios Resolvidos
A eficiência dos métodos de eliminação de Gauss e Gauss-Jordan pode ser comparada em termos do número de operações aritméticas (soma, subtração, multiplicação e divisão) necessárias para resolver um sistema linear de tamanho n. O método de Gauss requer aproximadamente (2n³/3) operações, enquanto o método de Gauss-Jordan requer aproximadamente (2n³/3 + n²) operações. Para sistemas grandes, a diferença torna-se significativa, sendo o Gauss ligeiramente mais eficiente.
| Tamanho do Sistema (n) | Operações (Gauss) (aproximado) | Operações (Gauss-Jordan) (aproximado) |
|---|---|---|
| 2 | (2*8)/3 ≈ 5 | (2*8)/3 + 4 = 8 |
| 3 | (2*27)/3 = 18 | (2*27)/3 + 9 = 27 |
| 10 | (2*1000)/3 ≈ 667 | (2*1000)/3 + 100 ≈ 767 |
Regra de Cramer
A regra de Cramer é um método para resolver sistemas lineares de n equações e n incógnitas, onde o determinante da matriz dos coeficientes é diferente de zero. Este método é computacionalmente caro para sistemas de grande porte, sendo mais eficiente para sistemas 2×2 e 3×3.
Para um sistema 2×2 da forma:
ax + by = c
dx + ey = f
A solução é dada por:
x = (ce – bf) / (ae – bd)
y = (af – cd) / (ae – bd)
Para um sistema 3×3, a solução envolve o cálculo de quatro determinantes: o determinante da matriz dos coeficientes e três determinantes obtidos substituindo cada coluna da matriz dos coeficientes pelo vetor dos termos independentes. A solução para cada variável é a razão entre o determinante correspondente e o determinante da matriz original.
Exemplo para um sistema 2×2: 2x + y = 8; x + 3y =
11. Aplicando a regra de Cramer:
x = (8*3 – 1*11) / (2*3 – 1*1) = 13/5
y = (2*11 – 8*1) / (2*3 – 1*1) = 14/5
Aplicações de Sistemas Lineares: Sistemas Lineares | Lista De Exercícios Resolvidos
Sistemas lineares são ferramentas matemáticas poderosas com amplas aplicações em diversas áreas do conhecimento. Sua capacidade de modelar relações entre variáveis de forma precisa e eficiente os torna essenciais para a resolução de problemas complexos em engenharia, economia e ciência da computação, entre outras disciplinas. A seguir, serão apresentados exemplos concretos que demonstram a versatilidade e a importância desses sistemas na modelagem e solução de problemas reais.
Exemplos de Aplicações em Diferentes Áreas
Sistemas lineares são utilizados para modelar e resolver problemas em diversas áreas, sendo sua aplicação frequentemente crucial para a obtenção de soluções eficazes e precisas. A formulação e resolução desses sistemas dependem da natureza do problema, mas o processo geralmente envolve a identificação das variáveis, a construção das equações lineares que representam as relações entre elas e, por fim, a solução do sistema resultante.
- Engenharia: Análise de circuitos elétricos. A Lei de Kirchhoff, por exemplo, estabelece relações lineares entre correntes e tensões em um circuito. Um sistema linear pode ser formulado para determinar as correntes em cada ramo do circuito, dadas as tensões e resistências. Considere um circuito simples com três malhas e três incógnitas (correntes). A aplicação das leis de Kirchhoff resulta em um sistema de três equações lineares com três incógnitas, que pode ser resolvido por métodos como eliminação de Gauss ou regra de Cramer.
- Economia: Modelagem de equilíbrio de mercado. Em um modelo simplificado de mercado com oferta e demanda, a quantidade ofertada e a quantidade demandada de um bem são funções lineares do preço. O ponto de equilíbrio de mercado, onde oferta e demanda se igualam, pode ser encontrado resolvendo um sistema linear de duas equações (oferta e demanda) com duas incógnitas (preço e quantidade).
- Ciência da Computação: Processamento de imagens. Imagens digitais são representadas por matrizes de pixels. Operações de processamento de imagem, como filtragem e compressão, podem ser formuladas como operações matriciais lineares. Por exemplo, a aplicação de um filtro de suavização a uma imagem pode ser representada como a multiplicação da matriz que representa a imagem por uma matriz que representa o filtro.
A solução deste sistema linear resulta na imagem filtrada.
Modelagem de Problemas Reais com Sistemas Lineares

A modelagem de problemas reais usando sistemas lineares envolve a identificação cuidadosa das variáveis relevantes e a formulação de equações lineares que capturam as relações entre elas. A solução do sistema fornece os valores dessas variáveis, que representam a solução do problema.
A precisão da solução depende da precisão da modelagem e da escolha do método de resolução. Erros de arredondamento numéricos podem afetar a solução, especialmente em sistemas grandes e mal-condicionados.
Em muitos casos, a simplificação do problema real para um modelo linear é uma aproximação. A validade desta aproximação deve ser avaliada cuidadosamente.
Exemplo de Problema de Mistura

Um químico precisa preparar 100 litros de uma solução de ácido clorídrico a 20% de concentração. Ele dispõe de duas soluções: uma a 10% e outra a 30%. Qual a quantidade de cada solução deve ser misturada para obter a solução desejada?Sejam x a quantidade (em litros) da solução a 10% e y a quantidade (em litros) da solução a 30%.
Podemos formular um sistema linear com duas equações:
x + y = 100 (equação da quantidade total)
0.10x + 0.30y = 0.20(100) = 20 (equação da concentração)
Resolvendo este sistema linear (por exemplo, usando o método da substituição ou eliminação), encontramos x = 50 litros e y = 50 litros. Portanto, o químico deve misturar 50 litros da solução a 10% com 50 litros da solução a 30% para obter 100 litros de solução a 20%.
Dominar a resolução de sistemas lineares é crucial para a progressão em diversas disciplinas científicas e de engenharia. Esta lista de exercícios, ao apresentar uma variedade de métodos e exemplos práticos, contribui para uma compreensão profunda e abrangente do tema. A análise comparativa dos métodos de resolução e a exploração de diferentes tipos de soluções fornecem uma base sólida para a resolução de problemas mais complexos e a modelagem de situações reais, preparando o leitor para aplicações futuras.

